Soh Cah Toa can be used through:
1. Angle of Elevation
The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (the line of sight)
The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (the line of sight)
Examples
Solving Problems Using Sine Function
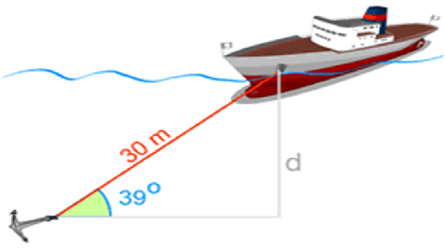
Example 1: Use the sine function to find "d"
We know
* The angle the cable makes with the seabed is 39°
* The cable's length is 30 m.
And we want to know "d" (the distance down).
Start with:
sin 39° = opposite/hypotenuse = d/30
Swap Sides:
d/30 = sin 39°
Use a calculator to find sin 39°:
d/30 = 0.6293…
Multiply both sides by 30:
d = 0.6293… x 30 = 18.88 to 2 decimal places.
The depth "d" is 18.88 m
(Retrieved from: http://www.mathsisfun.com/sine-cosine-tangent.html)
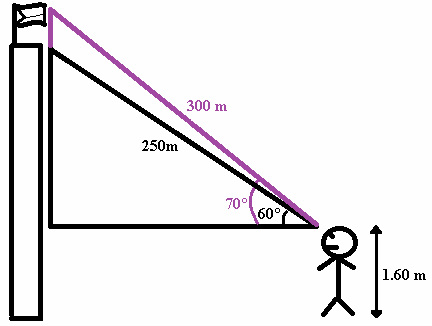
Example 2: What is the height of the flagpole?
Height of the building
Sin x= Opp/Hyp
Sin 60°= Opp/ 250
Opp= 250sin60°
Opp= 250 (.87)
Opp= 217.5 m
H of the bldg.= 217.5+1.60
H of the bldng. =219.1 m
Height of the building with the flagpole
Sin x= Opp/Hyp
Sin 70°= Opp/ 300
Opp= 300sin70° Height of the flagpole= 283.60-219.1 = 64.5 m
Opp= 300 (.94)
Opp= 282 m + 1.60
Opp= 283.60 m
Height of the building
Sin x= Opp/Hyp
Sin 60°= Opp/ 250
Opp= 250sin60°
Opp= 250 (.87)
Opp= 217.5 m
H of the bldg.= 217.5+1.60
H of the bldng. =219.1 m
Height of the building with the flagpole
Sin x= Opp/Hyp
Sin 70°= Opp/ 300
Opp= 300sin70° Height of the flagpole= 283.60-219.1 = 64.5 m
Opp= 300 (.94)
Opp= 282 m + 1.60
Opp= 283.60 m
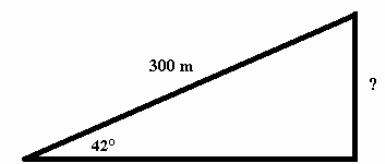
Example 3: A girl is flying her kite with 42° angle of elevation. If she knows the length of the string of her kite which is 300 m, how high is the kite? The triangle formed is shown on the left.
in x= opposite/hypotenuse
Sin42°= opposite/300
Opposite= 300sin42°
Opposite= 300(.67)
Opposite= 201 m
in x= opposite/hypotenuse
Sin42°= opposite/300
Opposite= 300sin42°
Opposite= 300(.67)
Opposite= 201 m
Solving Problems Using Cosine Function
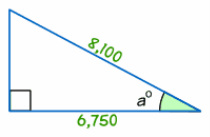
Example 1: Find the size of angle a°
inverse cos of 0.8333 = 33.6°
- Step 1 The two sides we know are Adjacent (6,750) and Hypotenuse (8,100).
- Step 2 Use Cosine Function.
- Step 3 Calculate Cos x= Adjacent / Hypotenuse = 6,750/8,100 = 0.8333
- Step 4 Find inverse cos of 0.8333:
inverse cos of 0.8333 = 33.6°
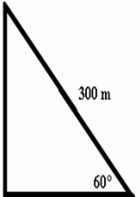
Example 2: What is the measure of the shorter side?
Cos x= adjacent/hypotenuse
Cos 60°= adjacent/300
Adjacent= 300cos60°
Adjacent= 300(0.5)
Adjacent= 150 m
Cos x= adjacent/hypotenuse
Cos 60°= adjacent/300
Adjacent= 300cos60°
Adjacent= 300(0.5)
Adjacent= 150 m
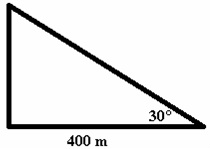
Example 3: What is the measure of the longest side of the triangle?
Cos x= adjacent/hypotenuse
Cos 30°= 400/hypotenuse
Hypotenuse= 400/cos30°
Hypotenuse= 400/0.87
Hypotenuse= 460 m
Cos x= adjacent/hypotenuse
Cos 30°= 400/hypotenuse
Hypotenuse= 400/cos30°
Hypotenuse= 400/0.87
Hypotenuse= 460 m
Solving Problems Using Tangent Function
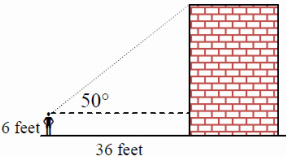
Example 1: Michael, whose eyes are six feet off the ground, is standing 36 feet away from the base of a building, and he looks up at a 50° angle of elevation to a point on the edge of building’s roof. To the nearest foot, how tall is the building?
Step 1: Make a detailed sketch of the situation. Make sure to include auxiliary horizontal lines as needed.
Step 1: Make a detailed sketch of the situation. Make sure to include auxiliary horizontal lines as needed.
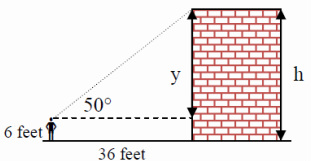
Step 2: Assign variables to represent the relevant unknowns. In this example, we shall use the variable y to represent the vertical leg of the right triangle, and h to represent the height of the building.
Step 3: Use SOHCAHTOA to solve for the unknown side of the right triangle:
tan 50° = y/36
y= 36tan50
y= 36(1.19)
y= 42.90 ft.
Step 4: Determine the height of the building: Since Michael’s eyes are six feet from the ground, we must add six feet to variable y to get h:
h= 6+y
h= 6+42.90
h= 48.90 ft.
Step 5: Check for reasonableness: If Michael were looking up at a 45° angle of elevation, y would be 36 feet due to the isosceles triangle created. Because he is looking up at a greater angle, it is reasonable that y is greater than 36 feet. Adding 6 feet accounts for the fact that his eyes are 6 feet from the ground.
Step 3: Use SOHCAHTOA to solve for the unknown side of the right triangle:
tan 50° = y/36
y= 36tan50
y= 36(1.19)
y= 42.90 ft.
Step 4: Determine the height of the building: Since Michael’s eyes are six feet from the ground, we must add six feet to variable y to get h:
h= 6+y
h= 6+42.90
h= 48.90 ft.
Step 5: Check for reasonableness: If Michael were looking up at a 45° angle of elevation, y would be 36 feet due to the isosceles triangle created. Because he is looking up at a greater angle, it is reasonable that y is greater than 36 feet. Adding 6 feet accounts for the fact that his eyes are 6 feet from the ground.
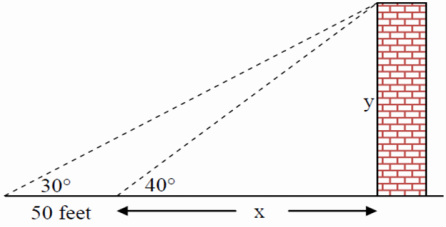
Example 2: An observer on the ground looks up to the top of a building at an angle of elevation of 30°. After moving 50 feet closer, the angle of elevation is now 40°. Consider the diagram.
a) Set up an equation representing the situation from the first vantage point. Your equation will incorporate the 30° angle, x, y, and the 50 feet.
b) Set up an equation representing the situation from the second vantage point. Your equation will incorporate the 40°, x, and y.
c) You now have two equations in two variables. Solve them simultaneously to determine the value of x, the distance from the second vantage point to the base of the building.
d) Solve for y, the height of the building.
Solution:
a) Set up an equation representing the situation from the first vantage point. Your equation will incorporate the 30° angle, x, y, and the 50 feet.
b) Set up an equation representing the situation from the second vantage point. Your equation will incorporate the 40°, x, and y.
c) You now have two equations in two variables. Solve them simultaneously to determine the value of x, the distance from the second vantage point to the base of the building.
d) Solve for y, the height of the building.
Solution:

(Retrieved from: www.MathWorksheetsGo.com)
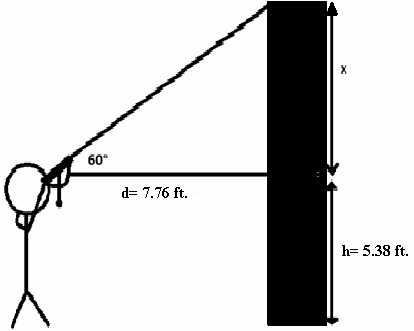
Example 3: Find the height of the building
Tan60°=x/d
1.73= x/7.76 ft.
x= 1.73 (7.76)
x= 13.42 ft
Height of post= x+h
H of post= 13.42 ft.+5.38 ft. Height of post= 18.8 ft.
Tan60°=x/d
1.73= x/7.76 ft.
x= 1.73 (7.76)
x= 13.42 ft
Height of post= x+h
H of post= 13.42 ft.+5.38 ft. Height of post= 18.8 ft.
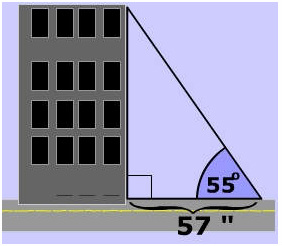
Example 4:
At 57" from the base of a building you need to look up at 55° to see the top of a building. What is the height of the building?
tan(55°)= opposite/hypotenuse
tan(55°) = height/57
height = 57 × tan(55°)
height= 57 (1.43)
height = 81"
At 57" from the base of a building you need to look up at 55° to see the top of a building. What is the height of the building?
tan(55°)= opposite/hypotenuse
tan(55°) = height/57
height = 57 × tan(55°)
height= 57 (1.43)
height = 81"
Solved Examples on Angle of Depression
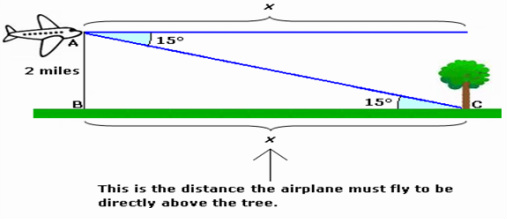
Example 1: An airplane is flying at a height of 2 miles above the level ground. The angle of depression from the plane to the foot of a tree is 15°. Find the distance that the air plane must fly to be directly above the tree.
Solution:
Step 1: Visualize the situation
Step 2: Let ‘x’ be the distance the airplane must fly to be directly above the tree.
Step 3: The level ground and the horizontal are parallel, so the alternate interior angles are equal in measure.
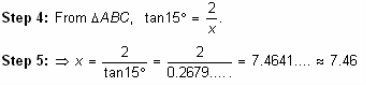
Step 6: So, the airplane must fly about 7.46 miles to be directly above the tree.
(Retrieved from: http://www.icoachmath.com/math_dictionary/angle_of_depression.html)
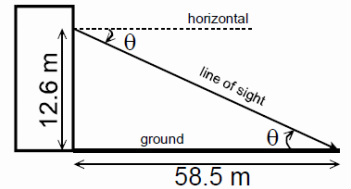
Example 2:
A person stands at the window of a building so that his eyes are 12.6 m above the level ground in the vicinity of the building. An object is 58.5 m away from the building on a line directly beneath the person. Compute the angle of depression of the person’s line of sight to the object on the ground.
Solution: The angle of depression of the line of sight is the angle, θ, that the line of sight makes with the horizontal, as shown in the figure to the right. Since the ground is level, it is parallel to any horizontal line, and so the angle that the line of sight makes with the ground is equal to θ as well. As a result, we have
tanθ= 12.6/58.5
θ= tan-1 (12.6/58.5)
θ= tan-1 (0.22)
θ= 12.40°
(Source: David W. Sabo, 2003 Angle of Elevation/Angle of Depression Page 2)
A person stands at the window of a building so that his eyes are 12.6 m above the level ground in the vicinity of the building. An object is 58.5 m away from the building on a line directly beneath the person. Compute the angle of depression of the person’s line of sight to the object on the ground.
Solution: The angle of depression of the line of sight is the angle, θ, that the line of sight makes with the horizontal, as shown in the figure to the right. Since the ground is level, it is parallel to any horizontal line, and so the angle that the line of sight makes with the ground is equal to θ as well. As a result, we have
tanθ= 12.6/58.5
θ= tan-1 (12.6/58.5)
θ= tan-1 (0.22)
θ= 12.40°
(Source: David W. Sabo, 2003 Angle of Elevation/Angle of Depression Page 2)
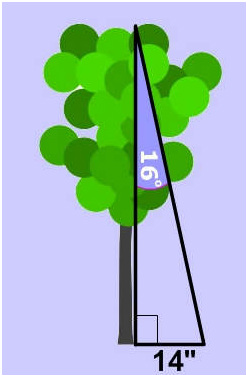
Example 3: What is the height of the tree on the left?
Tan(16°)= opposite/hypotenuse
tan(16°)= 14/height
height = 14/tan(16°)
height= 14/0.29
height= 48 "
Tan(16°)= opposite/hypotenuse
tan(16°)= 14/height
height = 14/tan(16°)
height= 14/0.29
height= 48 "
